Leetcode第73场双周赛解题报告

毕设完成后继续每天的刷题日常

1331. 数组序号转换

知识点：模拟

1. 首先使用快速排序，效率：$O(nlog_n)$
2. 然后按顺序将生成的排序数写入到哈希表
3. 对原序列进行遍历，从哈希表中读取没个数的序号，写入到答案数组中

/**
 * @param {number[]} arr
 * @return {number[]}
 */
var arrayRankTransform = function(arr) {
    const x = []
    arr.forEach(y=>x.push(y))
    arr.sort((a,b)=>a-b)
    let last = -1e9-1
    const ans = []
    let n = 0
    let mp = new Map()
    for(let i of arr) {
        if(i!==last) n++
        mp.set(i,n)
        last = i
    }
    for(let i of x) {
        ans.push(mp.get(i))
    }
    return ans
};

1328. 破坏回文串

知识点：归纳
效率：$O(n)$
如果这道题按照题目所说打大暴力，轮训所有位置进行替换，必然超时。

可以根据回文字符串性质：
给定一个字符$x$，我们要么将其替换为较小的字符，要么替换为较大的字符
较小的字符能够取到最小的即"a"，较大的字符能够取到最小的为$char(ascii(x+1))$

因为只能替换一个，因此我们想优先让较前的字符取a，如果没有字符能够更改为a，那么我们从后向前优先让字符替换为x+1。

/**
 * @param {string} palindrome
 * @return {string}
 */
var breakPalindrome = function(palindrome) {
    if(palindrome.length === 1) return ""
    let need = -1
    let n = ""
    let ans = ""
    for(let i = 0;i < Math.floor(palindrome.length/2);i++) {
        if(palindrome.charAt(i)!=="a") {
            need = i
            n = "a"
            break
        }
    }
    if(need < 0) {
        for(let i = palindrome.length-1;i >= Math.floor(palindrome.length/2);i--) {
            if(palindrome.charAt(i)!=="z") {
                need = i
                n = String.fromCharCode(palindrome.charCodeAt(i)+1)
                break
            }
        }
        
    }
    if(need >= 0) {
        palindrome
        for(let i =0;i < palindrome.length;i++){
            if(i!==need) {
                ans += palindrome.charAt(i)
            }else{
                ans += n
            }
        }
    }
    return ans
};

1329. 将矩阵按对角线排序

这道题用的超级暴力的解法，即构造一堆数组，排序后按序返回。
具体实现上，可以用栈取代记录idx

/**
 * @param {number[][]} mat
 * @return {number[][]}
 */
var diagonalSort = function(mat) {
    const [ny,nx] = [mat.length,mat[0].length]
    const arrs = []
    const startFrom = (x,y) => {
        const n = []
        while(x<nx&&y<ny) {
            n.push(mat[y][x])
            x++
            y++
        }
        arrs.push(n)
    }
    const startFrom1 = (x,y,arr) => {
        let idx = 0
        while(x<nx&&y<ny) {
            mat[y++][x++] = arr[idx++]
        }
    }
    for(let i = 0;i < nx;i++) {
        startFrom(i,0)
    }
    for(let i = 1;i < ny;i++) {
        startFrom(0,i)
    }
    console.log(arrs)
    for(let i = 0;i < arrs.length;i++) {
        arrs[i].sort((x,y)=>x-y)
    }
    
    let idx = 0
    for(let i = 0;i < nx;i++) {
        startFrom1(i,0,arrs[idx++])
    }
    for(let i = 1;i < ny;i++) {
        startFrom1(0,i,arrs[idx++])
    }
    console.log(arrs)
    return mat
};

1330. 翻转子数组得到最大的数组值

知识点：数学、贪心
这道题苦苦思索20min，首先发现了个规律：
设数列为$nums$，设原数列和为$sum_{original}$，新数列和为$sum_{new}$，交换位置为$l$、$r$，有如下式：
$sum_{new} = sum_{original} - |nums_{l-1} - sums_l| - |nums_{r+1} - sums_r| + |nums_{l-1} - sums_r| + |nums_{r+1} - sums_l|$
也就是说 新的和的计算只与两边的数有关，根据该推论写了个大暴力然后超时，代码如下，显然$O(n^2)$复杂度是不可行的：

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxValueAfterReverse = function(nums) {
    let sum = 0
    for(let i = 1;i < nums.length;i++)sum += Math.abs(nums[i]-nums[i-1])
    let mx = sum
    for(let i = 0;i < nums.length;i++)
        for(let j = i+1;j < nums.length;j++) {
            let tmp = sum
            if(i>0){
                tmp -= Math.abs(nums[i]-nums[i-1])
                tmp += Math.abs(nums[j]-nums[i-1])
            }
            if(j<nums.length-1){
                tmp -= Math.abs(nums[j+1]-nums[j])
                tmp += Math.abs(nums[j+1]-nums[i])
            }
            mx = Math.max(mx,tmp)
        }
    return mx
};

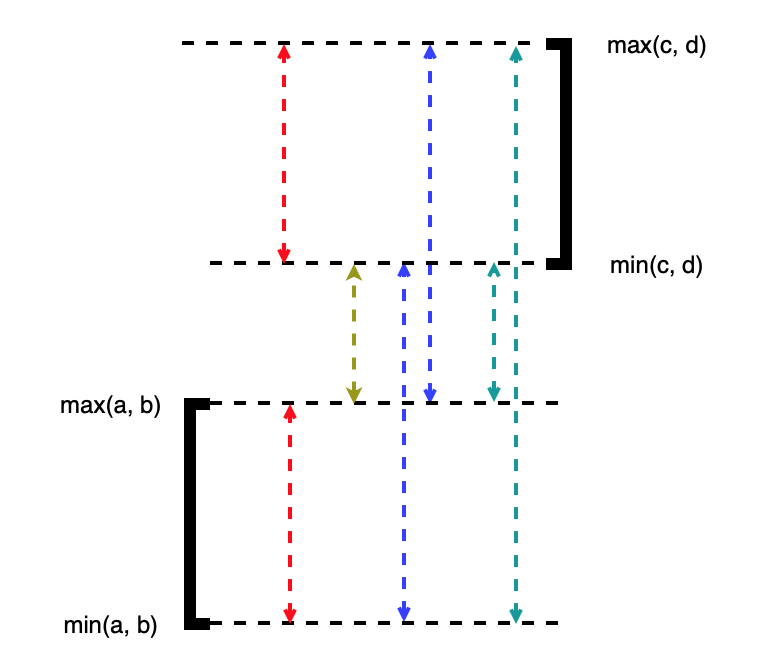
而后就参考题解了，国内的都是公式归纳，然而看不懂。
去国际站找到了非常棒的一篇，我认为解释的非常清楚了
简述之就是归纳了几种会出现的情况，最终发现，对于每两个相邻的数$nums_a$、$nums_b$，只需要进行如下操作：
$num1 = max(num1,min(nums_a,nums_b))$
$num2 = min(num2,max(nums_a,nums_b))$
即取所有数对的最大值的最小值，最小值的最大值，然后计算其差，根据的是下图：

最后，$delta = 2 * (num1-nums)$
所以，$sum_{new} = sum_{original} + delta$即为最大值
该思想可以使题目以$O(n)$的复杂度被解开

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxValueAfterReverse = function(nums) {
    let sum = 0
    let low = 100000000
    let high = -100000000
    for(let i = 1;i < nums.length;i++) {
        sum += Math.abs(nums[i]-nums[i-1])
        low = Math.min(low,Math.max(nums[i],nums[i-1]))
        high = Math.max(high,Math.min(nums[i],nums[i-1]))
    }
    console.log(low,high)
    let mx = sum
    if(high > low) mx+=2*(high-low)
    for(let i = 1;i < nums.length-1;i++) {
        mx = Math.max(mx,sum - Math.abs(nums[i+1]-nums[i]) + Math.abs(nums[i+1]-nums[0]))
        mx = Math.max(mx,sum - Math.abs(nums[i]-nums[i-1]) + Math.abs(nums[i-1]-nums[nums.length-1]))
    }
    return mx
};